Колко далеч можете да видите метеор?
>Получавам имейл.
Повечето задават въпроси от различен тип, повечето от които са доста лесни за отговор (всъщност на много може да се отговори чрез гугъл, намек за намек). Но понякога получавам въпрос, на който е по -трудно да се отговори, или дори такъв, на който съм се чудил за себе си, но така и не успях да разбера.
Така че бях доста заинтригуван, когато получих въпрос от Bad Reader Dean Lewis относно метеорите. По време на метеорния поток Персеиди през 2018 г. той беше далеч от семейството си, разделен на около 1000 километра. Ако беше видял метеор, възможно ли е да видят същия от по -далечното си местоположение?
Краткият отговор е: Да! Дългият отговор е ... математика. Готина, забавна математика.
И като се има предвид как, когато тази статия е публикувана, годишният метеорен поток на Геминид през 2018 г. достига върховете си тази вечер, мисля, че е подходящо да разберем това.
Астрономия на курсовия курс: Метеори, метеороиди и метеорити, О, Боже!
Ако Земята беше идеално плоска, тогава по принцип бихте могли да видите метеор чак до всеки ръб на Земята. Докато сте над земята, дори малко, тогава зрителната ви линия достига до всеки квадратен сантиметър от планетата от ваша страна, така че всеки метеор е видим за всички. В действителност въздухът не е напълно прозрачен, така че на известно разстояние гледате през толкова мръсотия, че не виждате нищо.
Земята обаче не е плоска. Сериозно! Кръгла е. И атмосферата го заобикаля като черупка, изтъняваща с височина и в крайна сметка излиза; тази височина зависи от вашето определение за пространство. Въпреки това, можем да изневерим малко, тъй като познаваме науката: Метеори като тези в душове са склонни да изгарят на около 100 километра над земята. Тази височина зависи от много неща, включително от това колко голяма е метеороиди (плътните частици междупланетни отломки, които се движат през пространството) са, колко бързо се движат, под какъв ъгъл навлизат в атмосферата и т.н. Но нека го наречем 100 км.
Най -близкият метеор може да бъде за вас, ако сте директно под него и след това е 100 км направо нагоре (във вашия зенит). Ако изгори по -далеч от зенита, значи трябва да е по -далеч от вас. Следователно най -далеч можете да видите метеор, разбира се, ако е точно на хоризонта.
Геометрията му изглежда така (забележка: НЕ в мащаб):
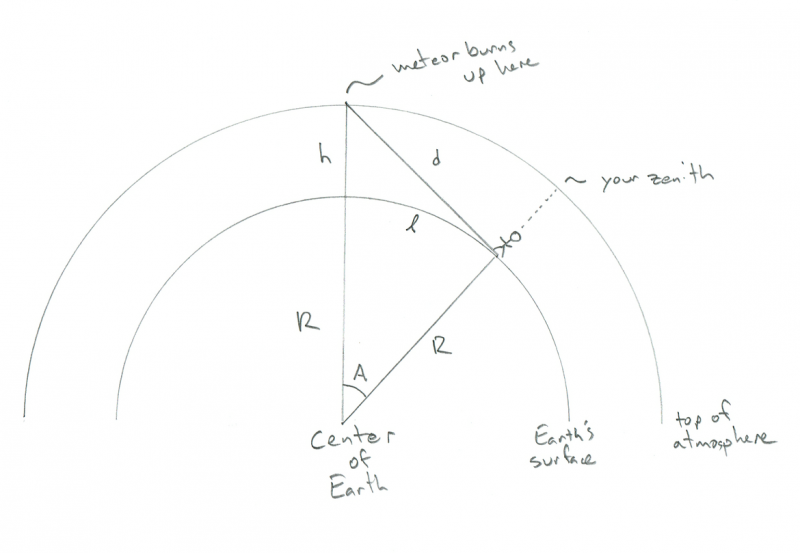
Схема, показваща геометрията на наблюдател, който наблюдава изгарянето на метеор. Кредит: Фил Плейт
Можете да видите човешката фигура, която стои на повърхността на извитата Земя - да речем, че това сте вие - с (също извитата) атмосфера над тях. В тази диаграма R е радиусът на Земята (6,4000 km), h е височината, която метеорът изгаря (100 km), а d е разстоянието от вас до метеора. A е ъгълът между позицията ви на Земята и позицията на метеора над нея, а курсивът l (както по дължина) е разстоянието, което трябва да изминете, за да бъде метеорът директно отгоре (знам, че това изглежда като странно нещо да искаш да знаеш, но бъди с мен). Странно, можете да изчислите всичко, от което се нуждаете, без да знаете d, но хайде, страхотно е да знаете колко далеч е метеорът, нали?
Ключът към всичко това е виждането, че ъгълът между метеора, вас и центъра на Земята е прав ъгъл. Това е така, защото метеорът е на хоризонта, както го виждате (или, ако предпочитате забавен жаргон, на допирателната линия на вътрешния кръг, където R го пресича). Това прави триъгълника правоъгълен триъгълник и ако си спомняте математиката си в гимназията, това означава, че можете да намерите всички страни и ъгли!
Помня питагорейската теорема ? В правоъгълен триъгълник квадратът с дължината на хипотенузата е равен на сумата от квадратите на другите две страни*. В нашия триъгълник хипотенузата е R+h, а другите страни са R и d.
Така
(R+h)2= d2+ R2
или, умножавайки лявата страна (използвайте ФОЛИЯ ):
медиите на здравия разум на острова на кучетата
R2+ 2Rh + h2 = d2+ R2
Решете за d, за да видите колко далеч е метеорът от вас. Обърнете внимание, че R2 е от двете страни, затова ги отменете, за да получите
д2= 2Rh + h2
Или
d = квадратен корен (2Rh + h2)
Е, ние знаем всички тези числа! Plug-n-chug, бебе:
d = квадратен корен (2 x 6400 x 100 + 10 000) = 1,136 km
Аха! Това означава, че ако видите метеор на хоризонта, той е на повече от 1100 километра! Това е дълъг път и технически най -далеч можете да видите метеор от земята.
Сега нека намерим курсив l. Първо трябва да знаем ъгъла А. Това изисква известна тригонометрия. Има много триг идентичности можете да използвате, за да разберете това, но моят любим†е, че в правоъгълен триъгълник синусът на ъгъл е дължината на противоположната страна, разделена на дължината на хипотенузата. Така че, ако получим това съотношение, можем да вземем обратния синус (или арксинус), за да получим ъгъла.
sin (A) = d / (R + h)
така
A = без-1(d / R + h)
Включете отново n-chug и получавам A = 10 °. Това е прилична част от земната повърхност!
И сега можем да получим курсив l. Около Земята има 360 °, а обиколката на Земята е 2 x pi x радиус = 40,192 km, така че има
40 192 км / 360 ° = 112 километра на градус
което означава от своя страна 10 ° = 1120 километра. Това е доста близо до d, което не е изненадващо. Рисунките са преувеличени, но в действителност въздушната обвивка над нас е малка в сравнение с размера на Земята. Ако направих чертежите в мащаб, ще видите, че d и l наистина са доста близки по дължина.
Добре, така че защо съм толкова горещ и притеснен да намеря l? Заради оригиналния въпрос! Ако сте забравили след тази математика, колко далеч могат да бъдат двама души и все още да виждат един и същ метеор?
Е, в този случай метеорът ще бъде директно между тях и на всеки от техните хоризонти. Тази геометрия изглежда така:
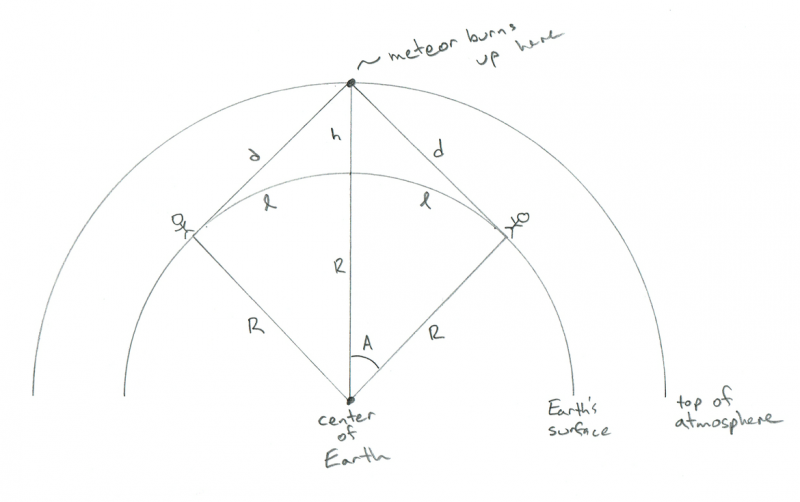
Схема, показваща геометрията на двама наблюдатели, гледащи как метеор изгаря точно между тях. Кредит: Фил Плейт
АХА! Сега виждате защо искам аз! Разстоянието между двамата е само 2 x l! Така че сега имаме отговора:
За да могат двама души да видят един и същ метеор, те могат да бъдат на не повече от 2 х 1 120 = 2 240 километра един от друг. Като пример, това е доста близо до разстоянието между Вашингтон, ДК и Денвър. Еха.
Между другото, за промяна на гледната точка (буквално), това означава от гледна точка на метеора, той може да види участък от Земята с ширина 2 240 километра (както в DC на източния край на Земята и Денвър на западния). Това е много готино.
И това ни води до действителния отговор на въпроса на Дийн: Ако той беше на 1000 км от семейството си, тогава да, технически те можеха да видят същия метеор. Какво ще кажете за това?
Това отново предполага, че въздухът е напълно чист и всичко това, което в действителност е по същество невъзможно. Така че тази математика представлява идеална ситуация (включително идеята, че метеорът е точно между тях).
Нека бъдем по -реалисти. Да предположим, че метеорът изгаря в небето на височина 45 ° над хоризонта и за двамата наблюдатели. Колко далеч биха били те един от друг? Е, отново ако приемем, че метеорът е точно между тях, геометрията е по -скоро такава:
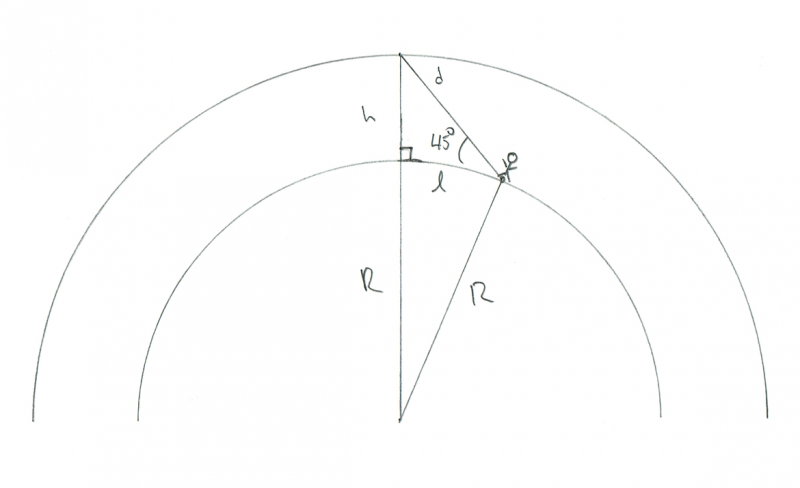
Схема, показваща геометрията на наблюдател, гледащ метеор, изгарящ на 45 ° над хоризонта. Кредит: Фил Плейт
Това всъщност е по -трудно за решаване, но знам още един трик: Ако приемем, че l е малък, тогава кривината на Земята няма да бъде важна. Например, ако искам да знам разстоянието между две дървета в моя двор, не ме интересува, че Земята е извита. На толкова малко разстояние мога да предположа, че е плоска. Нека направим това предположение тук.
В такъв случай имаме друг правоъгълен триъгълник, но този път правилният ъгъл е този под метеора. Дори го маркирах в диаграмата с малко квадратче. Така че, ако това е ъгъл от 90 ° и нашият ъгъл спрямо метеора е 45 °, тогава последният ъгъл (от метеора към наблюдателя) също е 45 °. Това означава, че това трябва да е равнобедрен триъгълник, така че l и h са еднакви! Тъй като знаем, че h е 100 км, значи трябва и l.
А това означава, че разстоянието между нашите двама наблюдатели е два пъти повече или 200 км.
Assassin's creed 2 здрав разум медии
Между другото, в този случай разстоянието до метеора е около 141 км. Ще оставя потвърждаването на това като упражнение на читателя.
По принцип това означава, че ако знаете колко високо от хоризонта е метеорът и височината, на която е изгорял, можете да изчислите разстоянието му (или ако знаете разстоянието, можете да получите височината му). Този триг обаче е доста сложен и мисля, че съм ви хвърлил достатъчно математика за днес.
Но е страхотно да се мисли, че малко математика в гимназията може да има такова забавно приложение. И ще призная, че е поетично и романтично да знаете, че докато раздялата не е твърде далеч, е възможно да споделите виждането на падаща звезда с някой друг. Каква прекрасна мисъл.
* В Магьосникът от Оз , плашилото се обърка след той има мозък.
† На разбира се Имам любима триг идентичност. Какво е твоето?













